Alligation Method
Just like Algebraic method, Alligation Alternate Method can be used for calculating strength of a solution obtained by mixing 2 or more solutions of different strengths. It is a visual method for computing proportions
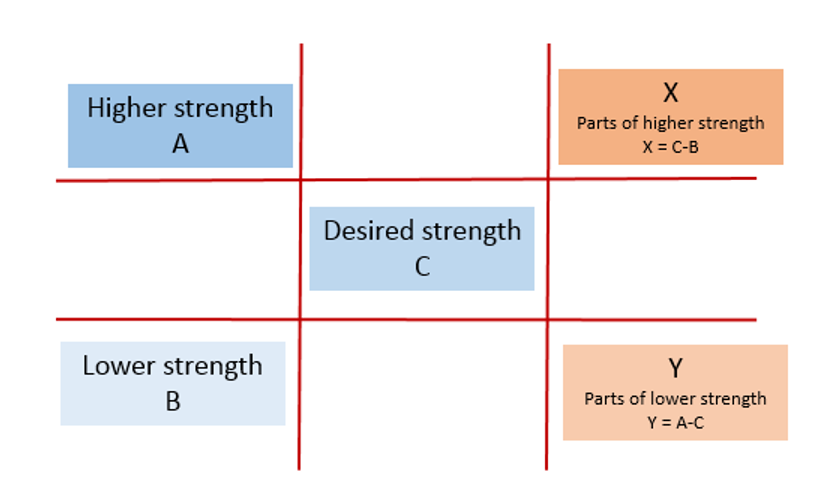
Steps:
- Make a tic-tac-toe grid.
- Enter the percentage strength of the higher strength solution in the upper left box.
- Enter the percentage strength of the lower strength solution in the lower left box.
- Enter the desired percentage strength in the center box.
- X is the unknown amount of higher strength solution to be mixed to obtain the desired strength.
- Y is the unknown amount of lower strength solution to be mixed to obtain the desired strength.
- Subtract B from C to solve for X.
- Subtract C from A to solve for Y.
- You will need X parts of A and Y parts of B to make X + Y parts of C.
- To convert parts to an actual volume amount, calculate as follows:
$$ Volume \ of \ Solution \ A = { x \ part \over x + y \ parts} \times desired \ volume \ of \ Solution \ C $$
$$ Volume \ of \ Solution \ B = { x \ part \over x + y \ parts} \times desired \ volume \ of \ Solution \ C $$
- Check your answer by adding the volume of solution A and the volume of solution B. The total should be the desired volume of solution C.
Let’s solve a problem using alligation method, which was solved earlier using the algebraic method.
|
Solved Problem: : In what proportions should 70 % dextrose and 10 % dextrose be mixed to make 1000 ml of 50 % dextrose? Approach: set up a tic-tac-toe grid which includes the higher, lower and desired strengths. 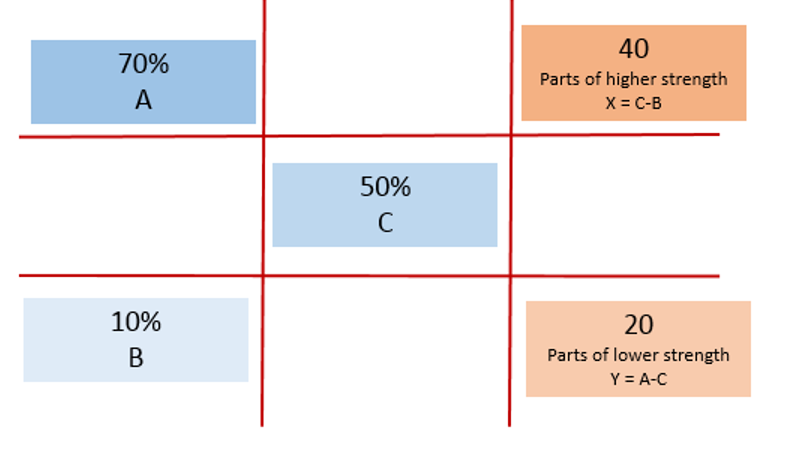
$$ Volume \ of \ Solution \ A = {x \ part \over x \ + \ y \ parts } \times desired \ volume \ of \ solution \ C $$ $$ Volume \ of \ Solution \ A = {40 \ parts \over 20 + 40 \ parts } \times 1000 \ ml$$ $$ Volume \ of \ Solution \ A = 667 \ ml$$ $$ Volume \ of \ Solution \ B = {y \ part \over x + y \ parts } \times desired \ volume \ of \ solution \ C$$ $$ Volume \ of \ Solution \ B = {20 \ parts \over 20 + 40 \ parts} \times 1000 \ ml $$ $$ Volume \ of \ solution \ B = 333 \ ml $$ Answer: Mix 667 ml of 70 % dextrose solution with 333 ml of 10 % dextrose solution to obtain 1000 ml of 50 % dextrose solution. |